Graph Ordering Attention Networks

Michail Chatzianastasis, Johannes Lutzeyer, George Dasoulas, Michalis Vazirgiannis

Published: AAAI 2023

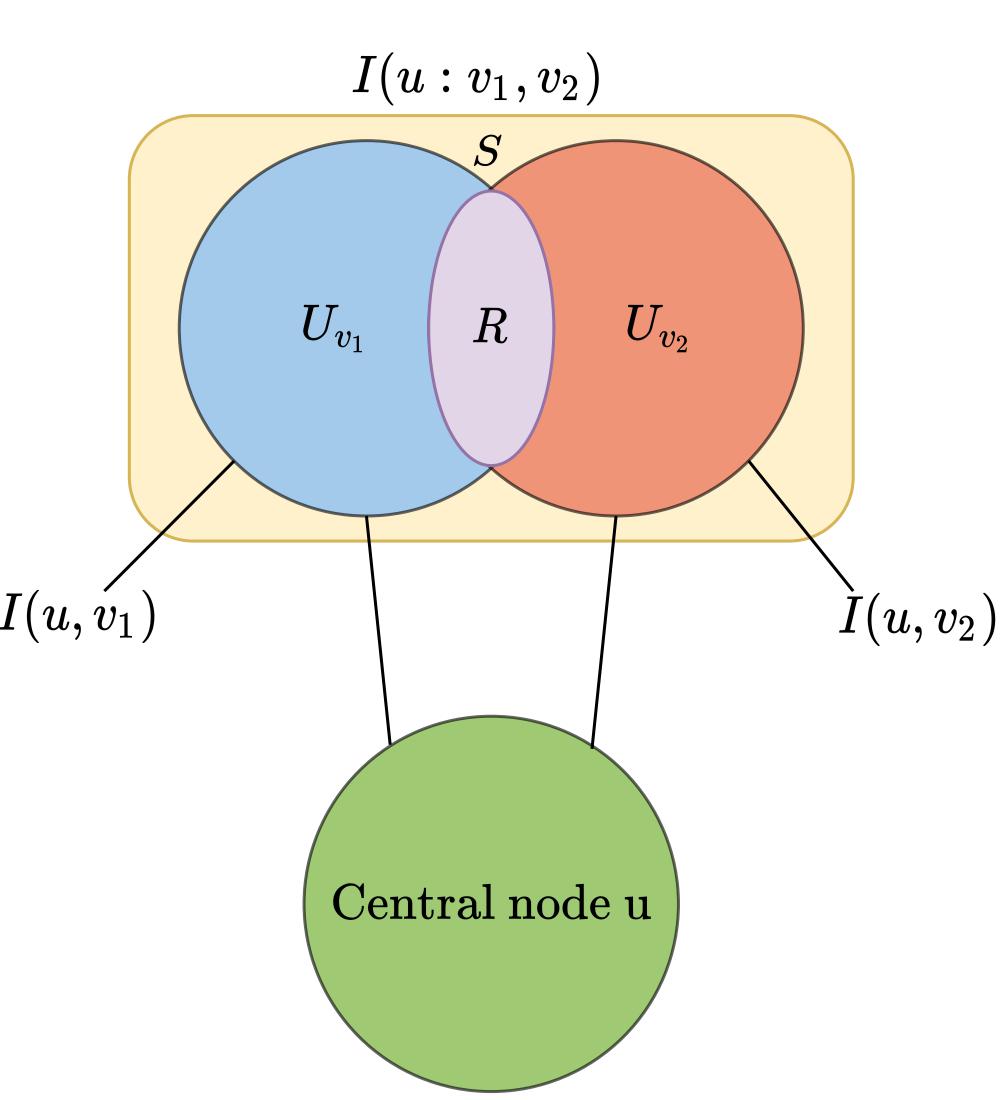
Graph Neural Networks (GNNs) have been successfully used in many problems involving graph-structured data, achieving state-of-the-art performance. GNNs typically employ a message-passing scheme, in which every node aggregates information from its neighbors using a permutation invariant aggregation function. Standard wellexamined choices like mean or sum aggregation functions have limited capabilities, as they are not able to capture interactions among neighbors. In this work, we formalize these interactions using an information-theoretic framework that notably includes synergistic information. Driven by this definition, we introduce the Graph Ordering Attention (GOAT) layer, a novel GNN component that captures higher-level dependencies between nodes in a neighborhood. This is achieved by learning local node orderings via an attention mechanism and processing the ordered representations using a recurrent neural network aggregator. This design allows us to make use of a permutation-sensitive aggregator while maintaining the permutation-equivariance of the proposed GOAT layer. The GOAT model demonstrates its increased performance in modeling graph metrics that capture complex information, such as the betweenness centrality and the effective size of a node. In practical use-cases, its superior modeling capability is confirmed through its success in several real-world node classification benchmarks.

An illustration of the Partial Information Decomposition for the case of one central node and two neighbors. The blue and the red circle represent the mutual information provided by the two neighbors about the central node. Each of these mutual information terms contains two atomic parts: $I(u:v_1)$ consists of the unique information in the $v_1$ neighbor $(U_{v_1}$, blue patch) and the information shared with $v_2$ neighbor ($R$, purple patch). Similarly, $I(u:v_2)$ consists of the unique information in $v_2$ neighbor ($U_{v_2}$, red patch) and again the shared information $R$. The joint mutual information $I(u : v_1,v_2)$ is represented by the yellow box encompassing the inner two circles. $I(u : v_1,v_2)$ consists of four elements: the unique information in $v_1$ neighbor, the unique information in $v_2$ neighbor, the redundant information among the two neighbors and additionally the synergistic information, $I(u : v_1,v_2) = U_{v_1} + U_{v_2} + R + S $